ZPU: The Zero-Knowledge Processing Unit

Published on:

Jul 3, 2023

TL;DR:

In this blog we propose the Zero Knowledge Processing Unit (ZPU), a versatile and programmable hardware accelerator, designed to address the emerging needs of ZKP processing.

We introduce the ZPU architecture and design considerations. We explain the design choices behind the different parts of the ZPU ecosystem: ISA, data-flow, memory and processing element (PE) internal structure. Finally, we compare to state-of-the-art ASIC architectures for ZK and Fully Homomorphic Encryption (FHE).

Introduction

The rapid growth of data-driven applications and the increasing need for privacy have led to a surge of interest in cryptographic protocols that protect sensitive information. Among these protocols, Zero-Knowledge Proofs (ZKPs) stand out as a powerful tool for ensuring both computation integrity and privacy. ZKPs enable one party to prove the validity of a statement to another party without revealing any additional information. This property has led to widespread adoption of ZKPs in diverse privacy focused applications, including blockchain technology, secure cloud computing solutions, and verifiable outsourcing services.

However, the adoption of ZKPs in real-world applications faces a major challenge: the performance overhead associated with proof generation. ZKP algorithms typically involve complex mathematical operations on very large integers, such as large-size polynomial computations and multi-scalar multiplications on elliptic curves. Moreover, cryptographic algorithms are constantly evolving, with new and more efficient schemes being developed at a rapid pace. As a result, existing hardware accelerators struggle to keep up with the diverse range of cryptographic primitives and the ever-changing landscape of cryptographic algorithms.

In this blog we propose the Zero Knowledge Processing Unit (ZPU), a novel and versatile hardware accelerator designed to address the emerging needs of ZKP processing. The ZPU is built on an Instruction Set Architecture (ISA) that allows for programmability, enabling it to adapt to the rapidly evolving cryptographic algorithms. The ZPU features an interconnected network of Processing Elements (PEs) with native support for large word modular arithmetic. The core structure of the PE is inspired by the Multiply-Accumulate (MAC) engine, which is a fundamental processing element in Digital Signal Processing (DSP) and other computing systems. The PEs’ operators are using modular arithmetic, with core components tailored to support the common operations in ZK algorithms, such as the NTT butterfly operation and elliptic curve point addition for multiscalar multiplication.

Instruction Set Architecture

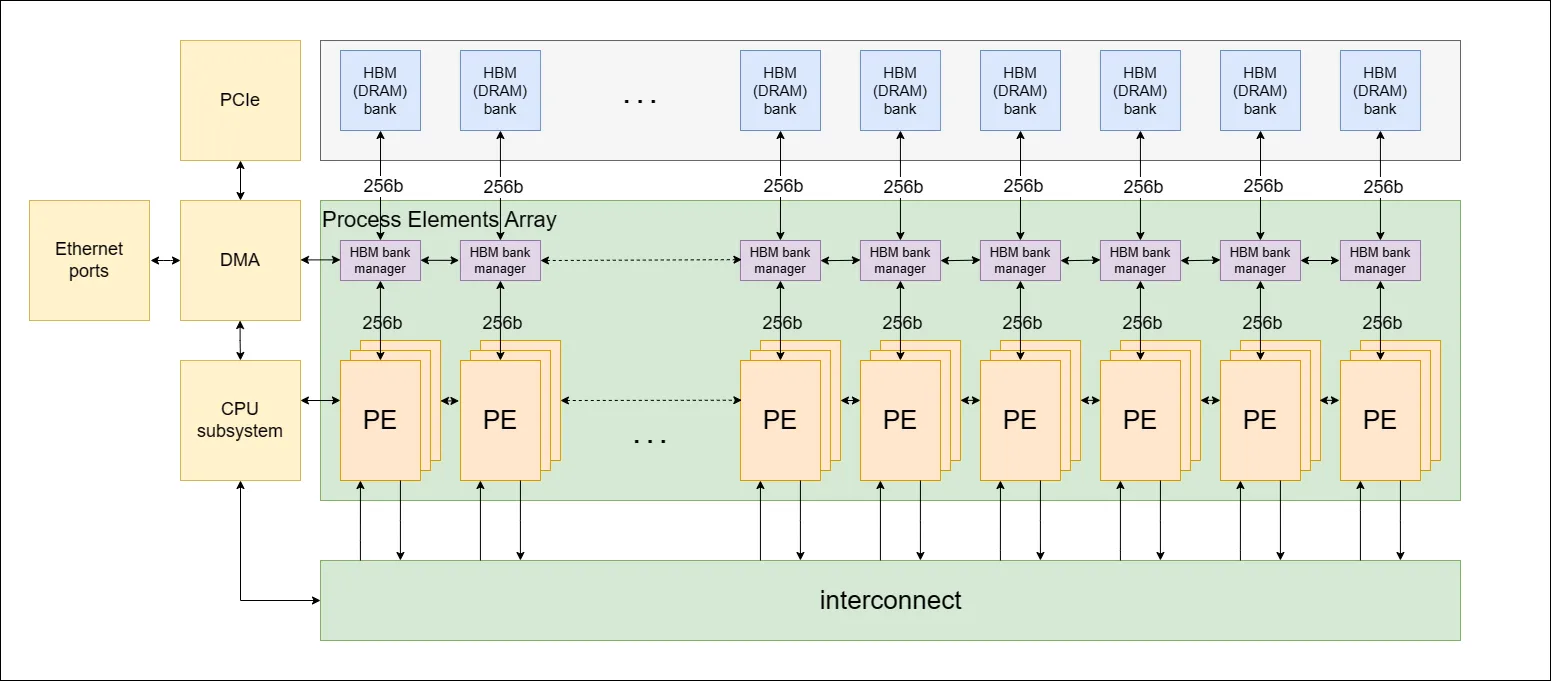
The ZPU architecture features an interconnected network of Processing Elements (PEs), Figure 1 below, defined by an Instruction Set Architecture (ISA). We chose this architecture to accommodate the changing landscape of zero-knowledge protocols.

The ISA approach allows the ZPU to remain flexible and adaptable to changes in ZK algorithms, as well as support a wide range of cryptographic primitives. Furthermore, utilizing an ISA rather than fixed hardware enables continued software improvement post-fabrication, ensuring that the ZPU stays relevant and efficient even as new advancements emerge in the field.

An ISA is a set of instructions that a processor can execute. It serves as an interface between the hardware and software, defining the way software interacts with the hardware. By designing the ZPU with a custom ISA, we can optimize it for the specific requirements of ZK processing tasks, such as large word modular arithmetic operations, elliptic curve cryptography, and other complex cryptographic operations.

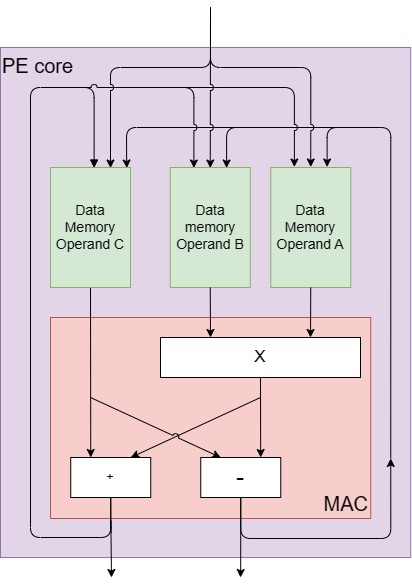
PE Core Components

Each PE is designed with a core that includes a modulo multiplier, an adder, and a subtractor, as shown in Figure 2. These core components are inspired by the fundamental processing element of Digital Signal Processing (DSP) and other computing systems, the Multiply-Accumulate (MAC) engine. The MAC engine efficiently performs multiply-accumulate operations, which involve multiplying two numbers and adding the product to an accumulator.

The PE’s core structure is tailored to serve the common operations in ZK, such as elliptic curve point addition for multi-scalar multiplication and NTT butterfly operation for Number Theoretic Transform (NTT). The butterfly operation involves an addition, a subtraction, and a multiplication, all under modulo arithmetic. This operation, which derives its name from the butterfly-like appearance of its computational flow diagram, is well-suited to the core hardware components of the PE, as they enable native butterfly computation through a dedicated butterfly instruction.

Additionally, each PE contains several specialized memory units, including:

Arrival Lounge: A memory for storing data arriving at the PE.
Departure Lounge: A memory for storing data departing from the PE.
Scratchpad Memory for Operands A, B, and C: Three separate memories for storing intermediate results.
Memory Extender: A multi-purpose memory for handling various algorithmic needs, such as bucket aggregation for multi-scalar multiplication (MSM).
Program Memory: A memory for storing the queue of instructions.

PE Bit Width

The PEs have native support for large word modular arithmetic operations (up to 256-bit words). The trade-off between high bit width native support and low bit width native support in a PE arises from the need to balance efficiency for different operand sizes.

When a PE has high bit width native support, it is optimized for handling large operand sizes without the need to break them down into smaller chunks. However, this optimization comes at the cost of reduced efficiency for smaller bit width operations, as the PE is underutilized. On the other hand, when a PE has low bit width native support, it is optimized for handling small operand sizes more efficiently. However, this optimization creates inefficiencies when processing larger bit width operations, as the PE needs to break down the larger operands into smaller chunks and process these chunks sequentially.

The challenge lies in finding the right balance between high and low bit width native support, which ensures efficient processing across a wide range of operand sizes. This balance should consider the common bit widths prevalent in the target application domain, which is ZK protocols, and weigh the benefits and drawbacks of each design choice. In the case of the ZPU architecture, a 256-bit word size was chosen as a good balance.

PE Connectivity

All PEs are connected through a ring connection, a topology in which each PE is directly connected to two neighboring PEs, forming a circular network. This ring connection allows control data to efficiently propagate between different PEs. The PEs are also connected via an Interconnect component, a mechanism similar to a barrel shifter, enabling direct connections between different PEs over time. This setup allows PEs to send and receive information from all other PEs.

Peripheral Components

The architecture also integrates an off-chip High Bandwidth Memory (HBM) to support high memory capacities and high memory bandwidth. Several PEs are clustered together to form a PE cluster, and each PE cluster is connected to one HBM bank or channel. Also, an ARM based on-chip CPU subsystem is included to manage overall system operations.

Performance Evaluation

To assess the performance of the ZPU, we have considered key operations fundamental to the algorithms we are aiming to accelerate. The principal operations we focused on are the NTT butterfly operation and the elliptic curve (EC) point addition operation. To evaluate the total compute time of our MSM and NTT operations, we calculated the total amount of compute instructions needed for them, and divided them by the clock frequency and the number of PEs.

The NTT butterfly operation is performed every clock cycle. For the elliptic curve point addition operation, a crucial element in multi-scalar multiplication (MSM), we deconstructed it into fundamental machine-level instructions that can be executed on a single PE. We subsequently calculated the number of clock cycles required for the completion of this operation. Through this analysis, we determined that each elliptic curve point addition operation can be executed every 18 clock cycles.

These assumptions provide a foundation for our performance evaluations, and can be adjusted as necessary to reflect different algorithmic requirements or hardware capabilities.

Based on our calculations, a configuration of only 72 PEs running at the GPU’s frequency 1.305 GHz would be adequate to match the performance of the GPU category winners in the Zprize’s MSM operation. Both Yrrid Software and Matter Labs achieved this feat, reaching a result of 2.52 seconds per four MSM computations using an A40 NVIDIA GPU. The comparison is based on the fixed-base point MSM computation involving 2²⁶ randomly chosen scalars from the BLS 12–377 scalar field, with a fixed set of elliptic curve points from the BLS 12–377 G1 curve and a randomly sampled input vector of finite field elements from the scalar field.

Based on our area estimations for the PEs, an ASIC using an 8nm process, identical to the process technology employed in the A40 GPU, can accommodate approximately 925 PEs within the same 628 mm2 area as the A40 GPU. This means we achieve a factor of approximately 13 times better efficiency than the A40 GPU.

PipeZK is an efficient pipelined accelerator designed to enhance the performance of Zero-Knowledge Proof (ZKP) generation, featuring dedicated MSM and NTT cores that optimize the processing of multi-scalar multiplications and large polynomial computations, respectively.

Compared to PipeZK, we found that a configuration of only 17 PEs running at PipeZK’s frequency 300 MHz would be adequate to match the performance of PipeZK for their MSM operation. PipeZK performs the MSM operation at 300 MHz on a 2²⁰ length MSM in the BN128 curve, taking 0.061 seconds to complete. Additionally, to match the performance of PipeZK for their NTT operation, running a 2²⁰ element NTT of 256-bit elements at 300MHz, which takes 0.011 seconds, we would need approximately 4 PEs running at the same frequency. In total, to match the performance of PipeZK running MSM and NTT in parallel, we would need 21 PEs.

According to our area estimations, an ASIC using a 28nm process, which is identical to the process technology employed in PipeZK , can house around 16 PEs within the same 50.75 mm2 area as the PipeZK chip. This means we are slightly less efficient than PipeZK’s fixed architecture (25% less efficient), while still being fully flexible to different elliptic curves and ZK protocols.

Ring Processing Unit (RPU) is a recent work designed to accelerate ring-based computations of Ring-Learning-with-Errors (RLWE), which is the foundation for various security and privacy-enhancing techniques, such as homomorphic encryption and post-quantum cryptography.

Compared to RPU, our calculations suggest that to match the performance of the RPU in its most optimized configuration (128 banks and HPLEs) when computing a 64K NTT of 128-bit elements, we would need approximately 23 PEs running at the RPU’s frequency 1.68GHz. Our analysis indicates that an ASIC, employing the same 12nm process technology as the RPU, can accommodate approximately 19.65 PEs within the 20.5 mm² area that the RPU occupies. This means we are slightly less efficient than the RPU (15% less efficient), while being compatible with primitives other than NTT.

TREBUCHET is a Fully Homomorphic Encryption (FHE) accelerator that uses Ring Processing Units (RPUs) as on-chip tiles. Tiles also facilitate memory management by scheduling data to be near computational elements. RPUs are replicated throughout the device, enabling software to minimize data movement and exploit data level parallelism.

Both TREBUCHET and ZPU are based on an ISA architecture and on large arithmetic word engines native to very long words (128-bit or above) under modular arithmetic. However, the added value of the ZPU over the RPU or the TREBUCHET SoC is that it broadens the set of problems that the architecture is designed to solve. While the RPU and TREBUCHET primarily focus on NTT, the ZPU supports more primitives, such as multi-scalar multiplication (MSM), and arithmetization — oriented hash functions.

Departing Words

Our performance evaluations have shown that the ZPU can match or even exceed the performance of existing state-of-the-art ASIC designs, while offering greater adaptability to changes in ZK algorithms and cryptographic primitives. While there are trade-offs to consider, such as the balance between high and low bit width native support in a PE, the ZPU’s design has been carefully optimized to ensure efficient processing across a wide range of operand sizes. For those interested in learning more about the ZPU, or exploring potential collaborations, please do not hesitate to reach out to us. We look forward to sharing more updates on our progress and future developments in the ZPU project.

We would like to thank Weikeng Chen for reviewing.